Area of a triangle

Understanding the area of a triangle is essential for various applications in mathematics, engineering, architecture, and everyday problem-solving. Calculating the area of a triangle can help in determining the amount of space within a triangular boundary, which is crucial for tasks such as land measurement, construction, and even art projects.

There are several methods to find the area of a triangle, each suited for different types of triangles and available measurements. The most common formula, known to many, is the basic formula where the area is calculated as half the product of the base and the height of the triangle. This method is straightforward and widely applicable, particularly for right triangles, where the height is easily identifiable.

However, not all triangles conveniently provide a clear base and height, especially when dealing with scalene triangles or those without a right angle. In such cases, more advanced methods like Heron's formula come into play. Heron's formula allows the calculation of the area when only the side lengths are known, making it extremely useful for a broader range of problems.

For triangles where angles are involved, the trigonometric formula offers a precise way to find the area using the lengths of two sides and the included angle. This method is particularly useful in trigonometry and applications requiring angular measurements, such as navigation and physics.

To ensure accuracy and efficiency in these calculations, using an area of a triangle calculator can be highly beneficial. These tools not only simplify the process but also help in visualizing the problem, ensuring no detail is overlooked.

In this guide, we will explore the different formulas for calculating the area of a triangle, including the basic formula, Heron's formula, and the trigonometric formula. We will also provide step-by-step instructions and examples to illustrate each method, making it easy for you to understand and apply these techniques. By the end of this guide, you will be equipped with the knowledge to calculate the area of any triangle, no matter its type or the measurements available.

Why Knowing the Area of a Triangle is Important

Understanding how to find the area of a triangle is not just a mathematical exercise; it has practical implications in various fields. For example, in the construction industry, precise measurements are crucial for creating accurate building plans and ensuring structural integrity. In land surveying, calculating the area helps in determining property boundaries and land use. Even in everyday life, knowing how to find the area of a triangle can assist in tasks like gardening or interior design, where space optimization is key.

Connecting Theory to Practice

By learning these methods, you can tackle a wide range of real-world problems. Whether you are a student aiming to excel in geometry, a professional needing precise measurements, or simply someone interested in math, mastering the area of a triangle is a valuable skill. This guide will serve as a comprehensive resource, helping you bridge the gap between theoretical knowledge and practical application.

What is a Triangle?

A triangle is one of the most fundamental shapes in geometry, characterized by three sides, three vertices, and three angles. This simple yet versatile shape is not only a cornerstone in mathematical studies but also appears frequently in various fields, from architecture to engineering.

Definition and Basic Properties

A triangle is a polygon with three edges and three vertices. It is the simplest form of a polygon, and its primary property is that the sum of its interior angles is always 180 degrees. This consistent property makes triangles a reliable shape for numerous geometric and trigonometric calculations.

Types of Triangles

Triangles can be categorized based on the lengths of their sides or the measures of their angles. Understanding these types is essential for applying the correct methods to calculate the area of a triangle.

Equilateral Triangle

• Definition: An equilateral triangle has all three sides of equal length, and all three interior angles are equal, each measuring 60 degrees.
• Properties: Due to its symmetry, the formula to find the area of an equilateral triangle is simplified to 

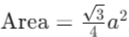
, where 𝑎 is the length of a side.

Isosceles Triangle

• Definition: An isosceles triangle has at least two sides of equal length. The angles opposite these sides are also equal.
• Properties: The height can be found using the Pythagorean theorem, which then allows for the use of the basic area formula Area=1/2×base×height
• Area=1/2 ​× base × height.

Scalene Triangle

• Definition: A scalene triangle has all sides of different lengths, and all interior angles are different.
• Properties: For scalene triangles, Heron's formula is particularly useful for finding the area when only the side lengths are known.

Right Triangle

• Definition: A right triangle has one angle that is exactly 90 degrees.
• Properties: The area of a right triangle can be easily calculated using the basic formula Area=1/2b x h, where the base and height are the two legs of the triangle.

Importance of Triangles in Geometry

Triangles are crucial in geometry because they form the basis for more complex shapes and structures. By understanding the properties and types of triangles, one can solve a wide range of problems involving angles, lengths, and areas. For instance, in trigonometry, triangles are used to define the trigonometric functions sine, cosine, and tangent, which are fundamental in analyzing periodic phenomena and solving real-world problems.

Triangles also play a significant role in other areas, such as:

• Construction and Architecture: Triangular shapes are used in trusses and frameworks due to their inherent stability and strength.
• Art and Design: Triangles contribute to aesthetic compositions and design elements.
• Navigation and Mapping: Triangles help in triangulation methods for determining distances and positions.

By mastering the basics of triangles, including their types and properties, you are well-equipped to delve deeper into calculating the area of a triangle using various formulas. This foundational knowledge is critical as we move forward to explore the different methods of determining the area based on the type and measurements of the triangle.

Types of Triangles

Understanding the various types of triangles is crucial for determining the appropriate method to calculate their area. Each type of triangle has unique properties that influence how you approach finding its area. Let's explore the different types of triangles, including right-angled, isosceles, and scalene triangles.

Right-Angled Triangle

A right-angled triangle, or right triangle, is characterized by having one of its angles exactly 90 degrees. This distinctive feature simplifies many geometric calculations, particularly when finding the area.

Properties:

• One angle is always 90 degrees.
• The side opposite the right angle is called the hypotenuse, which is the longest side.
• The other two sides are referred to as the legs of the triangle.

Area Calculation: The area of a right-angled triangle can be easily determined using the basic formula:

• Area=1/2×base×height

In a right-angled triangle, the base and the height are the two legs.

Example: If one leg of a right triangle is 3 units and the other leg is 4 units, the area would be:

Area=1/2×3×4=6 square units

Isosceles Triangle

An isosceles triangle has at least two sides of equal length. This symmetry affects both its internal angles and the methods used to calculate its area.

Properties:

• At least two sides are of equal length.
• The angles opposite the equal sides are also equal.

Area Calculation: For an isosceles triangle, the area can be calculated using the base and height, or by splitting the triangle into two right-angled triangles if the height is not directly given. The basic formula is:

Area=1/2×base×height

If only the sides are known, the height can be determined using the Pythagorean theorem.

Example: Consider an isosceles triangle with two sides of 5 units each and a base of 6 units. First, find the height:

• height=52−32=25−9=16=4 unitsheight=52−32​=25−9​=16​=4 units

Then, calculate the area:

• Area=12×6×4=12 square unitsArea=21​×6×4=12 square units

Scalene Triangle

A scalene triangle has all sides of different lengths and all interior angles different. This lack of symmetry requires a more flexible approach to find the area.

Properties:

• All three sides have different lengths.
• All interior angles are different.

Area Calculation: Heron's formula is particularly useful for scalene triangles when only the side lengths are known. Heron's formula states:

• Area=𝑠(𝑠−𝑎)(𝑠−𝑏)(𝑠−𝑐)

where s is the semi-perimeter:

• 𝑠=𝑎+𝑏+𝑐2​

Here, a, b, and c are the lengths of the sides.

Example: For a scalene triangle with sides 7 units, 8 units, and 9 units:

s=27+8+9​=12 units

Then, apply Heron's formula:

Area=12(12−7)(12−8)(12−9) 

=12×5×4×3=720 

≈26.83 square units

By understanding these types of triangles and their properties, you can apply the most suitable formula to calculate the area accurately. This foundational knowledge is essential as we progress to more advanced methods, ensuring you can handle any triangle you encounter.

Basic Formula for Area of a Triangle

Calculating the area of a triangle using the basic formula is straightforward and widely applicable, especially for right-angled and isosceles triangles. This method relies on knowing the base and height of the triangle, making it one of the most commonly used techniques in geometry.

Explanation of Terms

To effectively use the basic formula, it's essential to understand the key terms involved: "base" and "height."

Base: The base of a triangle is any one of its sides, typically the one chosen to be horizontal. It serves as the reference side for measuring the height. When the triangle is positioned with one side along a horizontal plane, that side is considered the base.

Height: The height (or altitude) of a triangle is the perpendicular distance from the base to the opposite vertex. It represents the shortest distance between the base and the top of the triangle. In a right-angled triangle, one of the legs can be treated as the height if the other leg is the base.

Basic Formula

The basic formula for calculating the area of a triangle is:

Area=12×base×heightArea=21​×base×height

This formula works by taking half of the product of the base and the height. The factor of one-half accounts for the fact that a triangle is essentially half of a parallelogram.

Step-by-Step Calculation

Identify the Base: Choose any side of the triangle to be the base. For convenience, it’s often easiest to select the horizontal side.

Measure the Height: Measure the perpendicular distance from the base to the opposite vertex. This distance should form a right angle with the base.

Apply the Formula: Multiply the base by the height, then divide the result by two to get the area of the triangle.

Examples

Example 1: Right-Angled Triangle Consider a right-angled triangle with a base of 5 units and a height of 12 units:

Area=12×5×12=30 square units

This calculation is straightforward as the legs of the right triangle directly provide the base and height.

Example 2: Isosceles Triangle An isosceles triangle with equal sides of 10 units and a base of 8 units can have its height calculated using the Pythagorean theorem. The height divides the base into two equal segments of 4 units each. Then, the height ℎh can be calculated as:

ℎ=102−42

=100−16=84

≈9.17 units

Now, apply the basic formula:

Area = 12×8×9.17

≈36.68 square units

Example 3: Scalene Triangle For a scalene triangle with a base of 7 units and a height of 4 units:

Area=12×7×4

=14 square units

The height in a scalene triangle can often be measured using geometric tools or derived from other known dimensions using trigonometric methods.

Understanding and applying the basic formula for the area of a triangle is fundamental for solving various geometric problems. This method's simplicity and versatility make it a vital tool in mathematics, applicable to different types of triangles under various conditions.

Basic Formula for Area of a Triangle

Calculating the area of a triangle using the basic formula is an essential skill in geometry. This method involves identifying the base and height of the triangle and applying a straightforward formula. Here’s a detailed, step-by-step guide to help you master this fundamental technique.

Step-by-Step Calculation

Identify the Base: The first step in finding the area of a triangle is to identify the base. The base is any one of the triangle's sides, but it is typically the side on which the triangle is imagined to be resting. For right-angled triangles, one of the legs is usually chosen as the base.

Measure the Height Perpendicular to the Base: Next, measure the height of the triangle. The height is the perpendicular distance from the base to the opposite vertex. This means the height forms a right angle with the base. In a right-angled triangle, the height is the other leg that is not chosen as the base. For isosceles and scalene triangles, the height might need to be measured using geometric tools or calculated using trigonometric methods.

Apply the Formula: Once the base and height are identified, apply the basic formula for the area of a triangle:

Area=1/2×base×height

This formula calculates the area by taking half of the product of the base and the height.

Examples to Illustrate the Process

Example 1: Right-Angled Triangle Suppose we have a right-angled triangle with a base of 6 units and a height of 8 units. To find the area:

Area=12×6×8=24 square units

In this case, the legs of the triangle serve as the base and height, making the calculation straightforward.

Example 2: Isosceles Triangle For an isosceles triangle with two equal sides of 10 units each and a base of 12 units, the height can be calculated first. The height divides the base into two equal segments of 6 units each. Using the Pythagorean theorem, the height ℎh is:

ℎ=102−62

=100−36

=64

=8 units

Now, applying the formula:

Area = 12×12×8 = 48 square units

Example 3: Scalene Triangle Consider a scalene triangle with a base of 9 units and a height of 5 units:

Area =12×9×5=22.5 square units

In a scalene triangle, where all sides and angles are different, the height is often measured using geometric tools.

Understanding and applying this basic formula is fundamental for solving various problems involving the area of a triangle. This straightforward method is applicable to different types of triangles, making it a versatile tool in geometry.

By mastering these steps, you can confidently calculate the area of any triangle, whether it’s a right-angled, isosceles, or scalene triangle. This foundational knowledge prepares you for more complex calculations, such as those involving Heron's formula or trigonometric methods, which we will explore in the following sections.

Heron's Formula

In geometry, there are times when you need to calculate the area of a triangle but only have the lengths of its sides. In such cases, Heron's formula becomes an invaluable tool. This formula allows you to find the area of any triangle when the lengths of all three sides are known, making it especially useful for scalene triangles, where no sides are equal.

Introduction to Heron's Formula

Heron's formula is named after Hero of Alexandria, an ancient Greek engineer and mathematician who derived this formula. It is particularly useful when you cannot easily measure the height of a triangle. This method is applicable to all types of triangles: equilateral, isosceles, and scalene.

Heron's formula provides a way to calculate the area based solely on the side lengths, without needing to find the height first. This makes it a versatile tool for various mathematical and practical applications.

Formula and Explanation

Heron's formula for the area of a triangle is given by:

Area=𝑠(𝑠−𝑎)(𝑠−𝑏)(𝑠−𝑐)

where 𝑠s is the semi-perimeter of the triangle, and 𝑎a, 𝑏b, and 𝑐c are the lengths of the sides. The semi-perimeter 𝑠s is calculated as:

𝑠=(𝑎+𝑏+𝑐)/2​

This formula works by first finding the semi-perimeter, which is half the perimeter of the triangle, and then using it in conjunction with the side lengths to determine the area.

Step-by-Step Calculation

Measure the Sides of the Triangle: Begin by measuring the lengths of all three sides of the triangle. Let's denote these sides as a, 𝑏, and 𝑐.

Compute the Semi-Perimeter: Calculate the semi-perimeter 𝑠s of the triangle using the formula:

1. 𝑠=(𝑎+𝑏+𝑐)/2​

Apply Heron's Formula: Use the semi-perimeter and the side lengths in Heron's formula to find the area:

1. Area=𝑠(𝑠−𝑎)(𝑠−𝑏)(𝑠−𝑐)

Example Calculation

Example: Consider a triangle with side lengths of 7 units, 8 units, and 9 units.

Step 1: Measure the sides:

𝑎=7,𝑏=8,𝑐=9

Step 2: Compute the semi-perimeter:

𝑠=7+8+92=12 units

Step 3: Apply Heron's formula:

Area=12(12−7)(12−8)(12−9)

=12×5×4×3=720≈26.83 square units

Heron's formula simplifies the process of finding the area of a triangle when the height is not easily accessible, and it’s particularly useful for scalene triangles. By understanding and applying this formula, you can tackle more complex geometric problems with confidence.

Trigonometric Formula

When dealing with triangles, there are scenarios where you know the lengths of two sides and the measure of the included angle. In such cases, the trigonometric formula for the area of a triangle becomes particularly useful. This formula leverages trigonometric functions to provide an accurate calculation of the area, making it an essential tool in trigonometry and practical applications like engineering and physics.

Introduction to Trigonometric Formula

The trigonometric formula is used to find the area of a triangle when you have the lengths of two sides and the included angle between them. This method is especially beneficial for non-right-angled triangles where traditional methods might not be straightforward. It is commonly applied in problems involving navigation, astronomy, and any field requiring precise measurements of angles and distances.

Formula and Explanation

The trigonometric formula for the area of a triangle is expressed as:

Area=1/2×𝑎×𝑏×sin⁡(𝐶)

where:

• a and b are the lengths of the two sides.
• C is the measure of the included angle between these sides.
• sin(C) is the sine of the included angle.

This formula calculates the area by taking half of the product of the two sides and the sine of the included angle. The sine function helps to account for the angle's impact on the overall area, providing an accurate measurement.

Step-by-Step Calculation

Measure the Sides and the Included Angle: Begin by measuring the lengths of the two sides 𝑎a and 𝑏b of the triangle, as well as the included angle 𝐶C. Ensure that the angle is measured in degrees or radians, depending on the sine function used.

Apply the Formula: Use the measured values in the trigonometric formula to find the area:

1. Area=1/2×𝑎×𝑏×sin⁡(𝐶)

Example Calculation

Example: Consider a triangle with sides a=7 units, b=9 units, and an included angle C=60∘.

Step 1: Measure the sides and the included angle:

𝑎=7 units, 𝑏=9 units, 𝐶=60∘

Step 2: Apply the formula:

• Area=12×7×9×sin⁡(60∘)

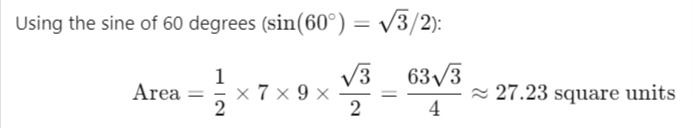
The trigonometric formula is particularly useful for triangles where it is difficult to measure the height directly. It provides a precise calculation based on the side lengths and the angle, making it a versatile tool in various scientific and engineering applications.

How to Use Hirequotient Area of Triangle Calculator

Using the Hirequotient Area of Triangle calculator simplifies the process of finding the area of a triangle, whether you have the base and height, the side lengths, or the included angle between two sides. This tool is designed to be user-friendly and efficient, providing quick and accurate results for various types of triangles. Here's a step-by-step guide on how to use the calculator effectively.

Step 1: Select the Formula

The first step is to choose the appropriate formula based on the information you have about the triangle. The calculator offers multiple options, including:

• Basic Formula: For triangles where the base and height are known.
• Heron's Formula: For triangles where the lengths of all three sides are known.
• Trigonometric Formula: For triangles where two sides and the included angle are known.

Step 2: Enter the Sides

Once you have selected the appropriate formula, enter the required dimensions:

• For the Basic Formula: Input the base and height of the triangle.
• For Heron's Formula: Input the lengths of all three sides of the triangle.
• For the Trigonometric Formula: Input the lengths of the two sides and the measure of the included angle.

The calculator interface is designed to be intuitive, with clear fields for each required measurement.

Step 3: Calculate

After entering the necessary values, simply click the "Calculate" button. The calculator will process the inputs and provide the area of the triangle. This instant calculation saves time and ensures accuracy, making it an invaluable tool for students, educators, and professionals alike.

Example Calculations

Using the Basic Formula:

• Input: Base = 5 units, Height = 10 units
• Process: Select the basic formula and enter the base and height.
• Result: The area will be calculated as: 

Area=1/2×5×10 

= 25 square units

Using Heron's Formula:

• Input: Side lengths = 6 units, 8 units, and 10 units
• Process: Select Heron's formula and enter the side lengths.
• Result: The area will be calculated using: 

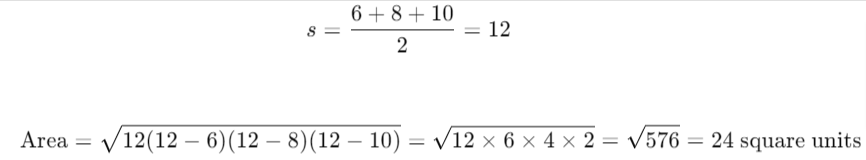
Using the Trigonometric Formula:

• Input: Sides = 7 units and 9 units, Included Angle = 45°
• Process: Select the trigonometric formula and enter the sides and angle.
• Result: The area will be calculated as: 

The Hirequotient Area of Triangle calculator is designed to handle various scenarios, ensuring that you can find the area accurately regardless of the triangle's type. This versatility makes it a powerful tool for educational purposes, professional use, and everyday problem-solving.

Benefits of Using Our Area of Triangle Calculator

Using the Hirequotient Area of Triangle calculator offers numerous advantages, making it an invaluable tool for anyone needing to calculate the area of a triangle accurately and efficiently. This section highlights the key benefits of the calculator, focusing on its accuracy, ease of use, efficiency, versatility, and educational value.

Accuracy

One of the primary benefits of the Hirequotient Area of Triangle calculator is its high accuracy. Calculating the area of a triangle manually can sometimes lead to errors, especially with complex formulas like Heron's formula or trigonometric calculations. The calculator ensures that each step is performed correctly, providing precise results every time. This accuracy is essential for academic purposes, professional applications, and any scenario where exact measurements are crucial.

Ease of Use

The user-friendly interface of the Hirequotient calculator makes it accessible to everyone, from students to professionals. The clear, straightforward design means that even those with limited mathematical knowledge can input values and get results effortlessly. The calculator guides users through each step, ensuring that all necessary information is provided for accurate calculations.

Efficiency

Time is often of the essence, and the Hirequotient Area of Triangle calculator excels in providing quick results. Manual calculations can be time-consuming, particularly when dealing with more complex triangles. By automating the process, the calculator saves valuable time, allowing users to focus on interpreting the results rather than performing the calculations. This efficiency is particularly beneficial in educational settings, where time can be better spent on understanding concepts rather than performing repetitive calculations.

Versatility

The calculator's versatility is another significant advantage. It supports various methods for finding the area of a triangle, including the basic formula, Heron's formula, and the trigonometric formula. This versatility means that users can calculate the area of any triangle type, whether it is equilateral, isosceles, scalene, or right-angled. This adaptability ensures that the calculator can handle a wide range of geometric problems, making it a reliable tool for different scenarios.

Educational Tool

Beyond its practical applications, the Hirequotient Area of Triangle calculator is an excellent educational tool. By using the calculator, students can gain a deeper understanding of geometric principles and the different methods for calculating the area of a triangle. The step-by-step guidance provided by the calculator helps reinforce learning, making it easier for students to grasp complex concepts. Additionally, by seeing how different formulas are applied, students can develop a stronger foundation in geometry.

Statistics and Real-World Applications

In real-world applications, accurate area calculations are vital. For example, in construction, precise measurements are necessary to ensure structural integrity and optimal use of materials. Using a reliable tool like the Hirequotient Area of Triangle calculator can help mitigate such risks by providing accurate measurements, thus contributing to more efficient and cost-effective project management.

The Hirequotient Area of Triangle calculator stands out for its accuracy, ease of use, efficiency, versatility, and educational value. Whether you are a student, educator, professional, or hobbyist, this tool will enhance your ability to calculate the area of a triangle quickly and accurately. By incorporating this calculator into your toolkit, you can ensure that your geometric calculations are always precise and reliable.

Example Calculations

To fully understand how to calculate the area of a triangle, it is helpful to look at detailed examples for each method: the basic formula, Heron's formula, and the trigonometric formula. These examples will illustrate the step-by-step process and demonstrate the versatility of each method.

Basic Formula Example

The basic formula for the area of a triangle is one of the simplest and most commonly used methods. It is particularly useful for right-angled and isosceles triangles where the base and height are easily identifiable.

Example: Consider a right-angled triangle with a base of 6 units and a height of 8 units. To find the area:

Identify the Base and Height:

• Base (𝑏) = 6 units
• Height (h) = 8 units

Apply the Formula:

Area=12×base×height

Area=21​×6×8

=24 square units

This straightforward calculation demonstrates the efficiency and simplicity of using the basic formula to find the area of a right-angled triangle.

Heron's Formula Example

Heron's formula is ideal for finding the area of a triangle when only the side lengths are known. This method is particularly useful for scalene triangles, where the sides are of different lengths.

Example: Consider a triangle with side lengths of 7 units, 8 units, and 9 units. To find the area:

Measure the Sides:

• Side a = 7 units
• Side b = 8 units
• Side c = 9 units

Compute the Semi-Perimeter:

𝑠=𝑎+𝑏+𝑐2=7+8+92=12 units

Apply Heron's Formula:

Area=𝑠(𝑠−𝑎)(𝑠−𝑏)(𝑠−𝑐)

 Area=12(12−7)(12−8)(12−9)

=12×5×4×3

=720​≈26.83 square units

This example highlights how Heron's formula can be used to accurately determine the area of a triangle based solely on its side lengths.

Trigonometric Formula Example

The trigonometric formula is useful when you know the lengths of two sides and the measure of the included angle. This method is applicable to various types of triangles and is particularly helpful in trigonometry.

Example: Consider a triangle with sides a=7 units and b=9 units, and an included angle C=45∘. To find the area:

Measure the Sides and the Included Angle:

• Side a = 7 units
• Side b = 9 units
• Included angle C = 45°

Apply the Trigonometric Formula:

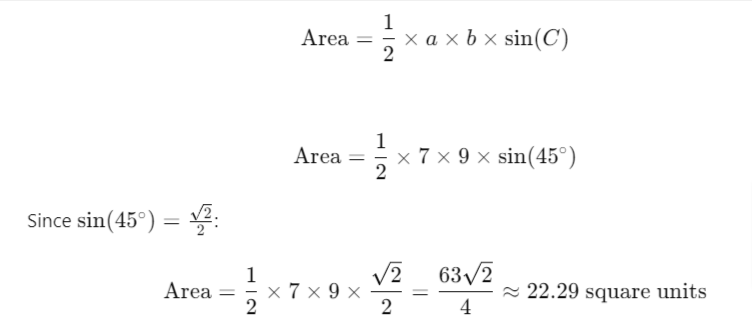
This example shows how the trigonometric formula can be applied to find the area of a triangle when the side lengths and included angle are known, offering a precise calculation method.

Special Cases

While the general methods for calculating the area of a triangle are versatile, certain types of triangles have unique properties that allow for simplified calculations. Here, we will explore special cases, including equilateral triangles, isosceles triangles, and right triangles. Understanding these specific scenarios will further enhance your ability to calculate the area of any triangle accurately and efficiently.

Equilateral Triangle

An equilateral triangle has all three sides of equal length and all three angles measuring 60 degrees. This symmetry allows for a simplified formula to calculate the area.

Simplified Formula: The area of an equilateral triangle can be calculated using the formula:

This simplified formula makes it easy to calculate the area of an equilateral triangle without needing to measure the height separately.

Isosceles Triangle

An isosceles triangle has at least two sides of equal length, and the angles opposite these sides are also equal. This property can be used to simplify the calculation of the area.

Calculating the Area: To find the area of an isosceles triangle, you can use the basic formula by first determining the height. The height can be calculated using the Pythagorean theorem if the base and the equal sides are known.

Example: Consider an isosceles triangle with two sides of 5 units each and a base of 6 units. First, calculate the height: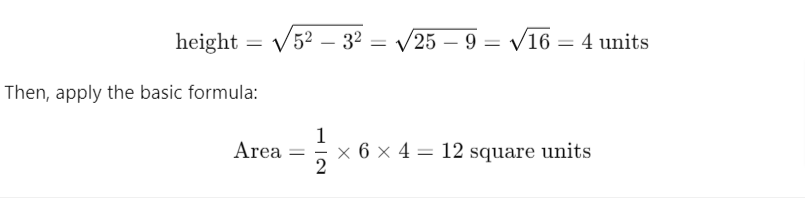

By leveraging the properties of isosceles triangles, you can simplify the process of finding their area.

Right Triangle

A right triangle has one angle that is exactly 90 degrees. The legs of the triangle can be directly used as the base and height, making the area calculation straightforward.

Straightforward Calculation: The area of a right triangle is found using the basic formula, where the legs of the triangle serve as the base and height:

Area=1/2×base×height

Example: For a right triangle with legs of 3 units and 4 units:

Area=12×3×4=6 square units

The simplicity of this calculation makes right triangles one of the easiest types to work with in geometry.

In conclusion, understanding how to find the area of a triangle is a fundamental skill in geometry that has practical applications across various fields. Whether you are dealing with an equilateral, isosceles, or right triangle, knowing the appropriate formulas and methods ensures accurate and efficient calculations.

FAQs: area of a triangle

How to find the area of a triangle?

To find the area of a triangle, use the formula: Area=1/2×base×height. Measure the base and the height of the triangle, then multiply them and divide by two.

How to find area of a triangle?

To find the area of a triangle, you can use the basic formula, Heron's formula, or the trigonometric formula, depending on the given information. The basic formula is the most commonly used and straightforward method.

How do you find the area of a triangle?

You find the area of a triangle by using the formula Area=1/2×base×height

This requires knowing the measurements of the base and the height of the triangle.

What is the area of a triangle?

The area of a triangle is the measure of the region enclosed by the triangle. It can be calculated using various formulas, with the most common being 1/2×base×height.

How to find the area of a right triangle?

To find the area of a right triangle, use the formula: Area=1/2×base×height,where the base and height are the two legs of the triangle.

How to find area of a right triangle?

Finding the area of a right triangle involves using the base and height, which are the two perpendicular sides. The formula is 1/2×base×height.

How to calculate the area of a triangle?

To calculate the area of a triangle, measure the base and height, then apply the formula: Area=1/2×base×height.

How to find an area of a triangle?

To find an area of a triangle, use the basic formula Area=1/2×base×height if you know the base and height, or use Heron's formula if you know all three sides.

How do you find area of a triangle?

You find the area of a triangle by multiplying the base by the height and then dividing by two, using the formula 12×base×height\frac{1}{2} \times \text{base} \times \text{height}21​×base×height

What is the formula for the area of a triangle?

The formula for the area of a triangle is Area=12×base×height\text{Area} = \frac{1}{2} \times \text{base} \times \text{height}Area=21​×base×height

How to calculate area of a triangle?

To calculate the area of a triangle, you need to know the base and height. Use the formula: Area=12×base×height\text{Area} = \frac{1}{2} \times \text{base} \times \text{height}Area=21​×base×height

How do I find the area of a triangle?

To find the area of a triangle, measure the base and height, then use the formula: Area=12×base×height\text{Area} = \frac{1}{2} \times \text{base} \times \text{height}Area=21​×base×height

Which figure best demonstrates the setup for the box method of finding the area of a triangle?

A rectangle divided into two equal right triangles best demonstrates the setup for the box method of finding the area of a triangle.

How to get the area of a triangle?

To get the area of a triangle, measure the base and height, then apply the formula Area=12×base×height\text{Area} = \frac{1}{2} \times \text{base} \times \text{height}Area=21​×base×height

How do you find the area of a right triangle?

To find the area of a right triangle, use the formula Area=12×base×height\text{Area} = \frac{1}{2} \times \text{base} \times \text{height}Area=21​×base×height where the base and height are the two legs of the triangle.

What is the formula for area of a triangle?

The formula for the area of a triangle is Area=12×base×height\text{Area} = \frac{1}{2} \times \text{base} \times \text{height}Area=21​×base×height

How to find the surface area of a triangle?

To find the surface area of a triangle, you typically refer to the area using the formula Area=12×base×height\text{Area} = \frac{1}{2} \times \text{base} \times \text{height}Area=21​×base×height

How do u find the area of a triangle?

You find the area of a triangle by measuring the base and height, then applying the formula 12×base×height\frac{1}{2} \times \text{base} \times \text{height}21​×base×height

How to find the area of a triangle with 3 sides?

To find the area of a triangle with 3 sides, use Heron's formula: Area=s(s−a)(s−b)(s−c)\text{Area} = \sqrt{s(s - a)(s - b)(s - c)}Area=s(s−a)(s−b)(s−c)​ where sss is the semi-perimeter.

What is the formula to find the area of a triangle?

The formula to find the area of a triangle is 12×base×height\frac{1}{2} \times \text{base} \times \text{height}21​×base×height

How to find surface area of a triangle?

To find the surface area of a triangle, use the basic area formula 12×base×height\frac{1}{2} \times \text{base} \times \text{height}21​×base×height for its two-dimensional space.

How to do area of a triangle?

To do the area of a triangle, use the formula 12×base×height\frac{1}{2} \times \text{base} \times \text{height}21​×base×height and input the measurements for the base and height.

What is the area of a right triangle?

The area of a right triangle is calculated using the formula 12×base×height\frac{1}{2} \times \text{base} \times \text{height}21​×base×height where the base and height are the two perpendicular sides.

What is the formula for the area of a triangle?

The formula for the area of a triangle is 1/2×base×height.

What is the formula for finding the area of a triangle?

The formula for finding the area of a triangle is 1/2×base×height.

What is area of a triangle?

The area of a triangle is the space enclosed by its three sides, calculated using the formula 1/2×base×height

What is the formula for finding the area of a triangle?

The formula for finding the area of a triangle is 1/2×base×height.

How to solve area of a triangle?

To solve the area of a triangle, measure the base and height, then apply the formula 1/2×base×height.

How to find the area of an equilateral triangle?

To find the area of an equilateral triangle, use the formula 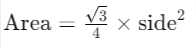where the side is the length of one of the triangle's sides.

How to get area of a triangle?

To get the area of a triangle, measure the base and height, then use the formula 1/2×base×height

How to solve the area of a triangle?

To solve the area of a triangle, measure the base and height, and then apply the formula 1/2×base×height.

How to find area of a non-right triangle?

To find the area of a non-right triangle, use Heron's formula if you know all three sides, or the trigonometric formula if you know two sides and the included angle.

How to find area and perimeter of a triangle?

To find the area, use 1/2×base×height.

What is the area of a triangle formula?

The area of a triangle formula is 1/2×base×height.

What is an area of a triangle?

An area of a triangle is the region enclosed by the three sides, calculated using 1/2×base×height.

How to find the area of a triangle with coordinates?

To find the area of a triangle with coordinates, use the formula: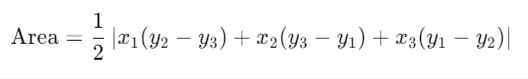

How do you find an area of a triangle?

You find an area of a triangle by using the formula 1/2×base×height.

How do you find an area of a triangle?

You find an area of a triangle by using the formula 1/2×base×height.

How to find the area of a triangle formula?

To find the area of a triangle formula, understand that it involves multiplying the base by the height and then dividing by two. The formula is 1/2×base×height.

How to calculate the area of a right triangle?

To calculate the area of a right triangle, use the formula 1/2×base×height where the base and height are the two legs forming the right angle.

How to find the area and perimeter of a triangle?

To find the area, use the formula 1/2×base×height. For the perimeter, add up the lengths of all three sides: Perimeter=a+b+c

How to find the height of a triangle without the area?

To find the height of a triangle without knowing the area, you can use trigonometric ratios or the Pythagorean theorem if the triangle is right-angled, or rearrange the area formula if you know the area: height=(2×Area)/base.

How to calculate area of a right triangle?

To calculate the area of a right triangle, apply the formula 1/2×base×height. The base and height are the two perpendicular sides.

How to figure out the area of a triangle?

To figure out the area of a triangle, measure the base and the height, then use the formula 1/2×base×height.

How to find the surface area of a triangle prism?

To find the surface area of a triangular prism, calculate the area of the two triangular bases and the areas of the three rectangular sides, then sum them up: Surface Area=2×Area of Triangle+Perimeter of Triangle×Length of Prism

What is the area of the equilateral triangle with the length of each side equal to a?

The area of an equilateral triangle with side length a is given by the formula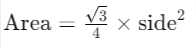

How to find area of a triangle without height?

To find the area of a triangle without the height, use Heron's formula: Area=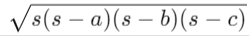 where s is the semi-perimeter.

How to find the area of an isosceles triangle?

To find the area of an isosceles triangle, use the formula 1/2×base×height. If the height is unknown, you can calculate it using the Pythagorean theorem.

A triangle base is 6 inches long and its height is 5 inches. What is the area of the triangle?

For a triangle with a base of 6 inches and a height of 5 inches, the area is calculated as: Area=12×6×5=15 square inches

How do you find the area of a triangle?

To find the area of a triangle, measure the base and height, then apply the formula 1/2×base×height.

How to find the surface area of a triangle prism?

To find the surface area of a triangular prism, calculate the area of the two triangular bases and add the areas of the three rectangular sides. The total surface area is: Surface Area=2×Area of Triangle+Perimeter of Triangle×Length of Prism

How do you get the area of a triangle?

You get the area of a triangle by using the formula 1/2×base×height.

How to find the area of a non-right triangle?

For a non-right triangle, you can use Heron's formula if you know all three sides: Area=​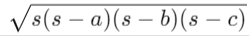, or the trigonometric formula if you know two sides and the included angle.

How to find area of an equilateral triangle?

To find the area of an equilateral triangle, use the formula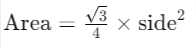

What is the formula for area of a triangle?

The formula for the area of a triangle is 1/2×base×height.

How to find an area of a right triangle?

To find the area of a right triangle, use the formula 1/2×base×height where the base and height are the two perpendicular sides.

How to find the area of a triangle prism?

To find the area of a triangle prism, you need to calculate the area of the triangular base using 1/2×base×heightand then use this to find the volume and surface area of the prism.

How do I find the area of a right triangle?

To find the area of a right triangle, measure the base and height, then use the formula 1/2×base×height

How do you calculate the area of a triangle?

You calculate the area of a triangle by using the formula 1/2×base×height

How to find area of a triangle with 3 sides?

To find the area of a triangle with 3 sides, use Heron's formula: Area=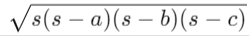

where s is the semi-perimeter of the triangle.

What is the area of a triangle?

The area of a triangle is the measure of the space enclosed by its three sides, typically calculated using the formula 1/2×base×height.

How to find the area of a triangle calculator?

To find the area of a triangle using a calculator, input the base and height values into the area formula 1/2×base×height, or use a specific triangle area calculator that can handle different formulas.

How to get the area of a right triangle?

To get the area of a right triangle, apply the formula 1/2×base×height

How to solve for area of a triangle?

To solve for the area of a triangle, measure the base and height, and use the formula 1/2×base×height

How do you find the surface area of a triangle?

The surface area of a triangle is the same as its area and is calculated using 1/2×base×height

How to find the area of a triangle without the height?

If the height is unknown, use Heron's formula for the area if the side lengths are known: 

Area=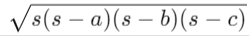

where s is the semi-perimeter.

How do you find area of a right triangle?

You find the area of a right triangle by using the formula 1/2×base×height.

What is the formula for the area of a right triangle?

The formula for the area of a right triangle is 1/2×base×height.

How to figure area of a triangle?

To figure the area of a triangle, use the formula 1/2×base×height.

How do u find area of a triangle?

You find the area of a triangle by measuring the base and height, then using the formula 1/2×base×height.

How to find the perimeter and area of a triangle?

To find the area, use 12×base×height\frac{1}{2} \times \text{base} \times \text{height}21​×base×height. For the perimeter, add up the lengths of all three sides: Perimeter=a+b+c\text{Perimeter} = a + b + cPerimeter=a+b+c

How to find the area of a triangle on a graph?

To find the area of a triangle on a graph, you can use the coordinates of the vertices and apply the formula:

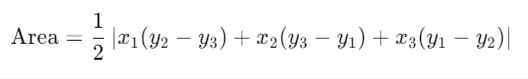
This method is useful for triangles plotted in a coordinate plane.

What is the area of this triangle? a. b. c. d. e.

To determine the area of a triangle given multiple choice options (a, b, c, d, e), identify the base and height from the provided information, then use the formula 1/2×base×height.

How to figure the area of a triangle?

To figure the area of a triangle, measure the base and height, then use the formula 1/2×base×height

How to find the area of a triangle with 2 sides and an angle?

To find the area of a triangle with 2 sides and an included angle, use the trigonometric formula:

Area=1/2×a×b×sin⁡(C)

where a and b are the sides, and C is the included angle.

How to find the area of a scalene triangle?

For a scalene triangle, use Heron's formula if you know the lengths of all three sides:

Area=s(s−a)(s−b)(s−c)

where s is the semi-perimeter.

Given a triangle with a base of 8 units and a height of 6 units, what is its area?

The area of a triangle with a base of 8 units and a height of 6 units is:

Area=1/2×8×6= 24 square units

How to find the area of an obtuse triangle?

To find the area of an obtuse triangle, use the basic formula 1/2×base×height or Heron's formula if the side lengths are known.

How to find perimeter and area of a triangle?

To find the area, use 

1/2×base×height.

For the perimeter, sum the lengths of all three sides: Perimeter=a+b+c

How find the area of a triangle?

To find the area of a triangle, measure the base and height, then use the formula 1/2×base×height

How to do the area of a triangle?

To find the area of a triangle, measure the base and height, and then apply the formula 1/2×base×height

How to figure out area of a triangle?

To figure out the area of a triangle, measure the base and height, and then use the formula 1/2×base×height.

The formula for the area of a triangle is , where b is the length of the base and h is the height.

The formula for the area of a triangle is:

Area=12×base×height

How do you find the area of a non-right triangle?

To find the area of a non-right triangle, use Heron's formula if you know all three sides, or the trigonometric formula if you know two sides and the included angle.

How to find the area of a triangle?

To find the area of a triangle, use the formula 1/2×base×height if you know the base and height, or use Heron's formula if you know the side lengths.

How to find the area of a triangle that is not a right triangle?

For a triangle that is not a right triangle, use Heron's formula:

Area=s(s−a)(s−b)(s−c)

where sss is the semi-perimeter.

What is the area of triangle PQR? Round to the nearest tenth of a square unit.

To find the area of triangle PQR, use the given dimensions and apply the appropriate formula (basic formula, Heron's formula, or trigonometric formula), then round the result to the nearest tenth.

How to find height of a triangle without area?

To find the height of a triangle without knowing the area, you can use trigonometric ratios if you have the lengths of the sides or rearrange the area formula if you know the area and the base.

How to find the area of a triangle on a coordinate plane?

To find the area of a triangle on a coordinate plane, use the formula:

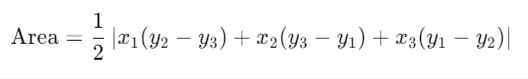
What is the area of a triangle with side lengths 30, 40, and 50?

To find the area of a triangle with side lengths 30, 40, and 50, use Heron's formula:

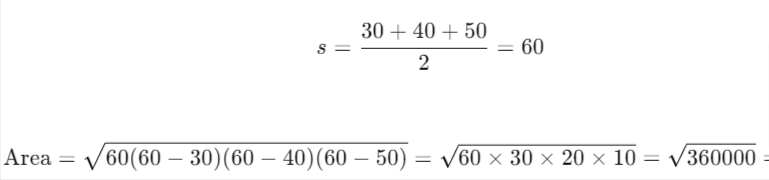
What is the area of an equilateral triangle?

The area of an equilateral triangle is given by the formula:

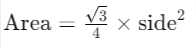
What is the area of an acute isosceles triangle with a base of 5 and height of 9?

For an acute isosceles triangle with a base of 5 and a height of 9, the area is:

Area=12×5×9=22.5 square units

How do u find the area of a right triangle?

To find the area of a right triangle, use the formula 1/2×base×height, where the base and height are the two legs forming the right angle.

What is the equation for the area of a triangle?

The equation for the area of a triangle is:

Area=1/2×base×height.

How to find area of a triangle with coordinates? Points x(6,8)x(6,8)x(6,8), y(3,3)y(3,3)y(3,3), and z(13,−3)z(13,-3)z(13,−3) form a triangle. What is the area of △xyz?

How to find the base of a triangle without the area?

To find the base of a triangle without knowing the area, use trigonometric ratios or the Pythagorean theorem if the height and other side lengths are known.

How to find the surface area of a 3D triangle?

For a 3D triangular surface (like a triangular pyramid), you need to calculate the area of each triangular face and then sum them.

What is the formula for finding the area of a right triangle?

The formula for finding the area of a right triangle is:

Area=1/2×base×height

What is the area of a triangle?

The area of a triangle is the measure of the space enclosed by its three sides. It is calculated using the formula 1/2×base×height.

How to get area of a right triangle?

To get the area of a right triangle, use the formula 1/2×base×height. Measure the two perpendicular sides, which are the base and the height, then apply the formula.

How to find the area of a 90 degree triangle?

The area of a 90-degree triangle, or a right triangle, is found using the formula 1/2×base×height. The base and height are the two sides that form the right angle.

How to find area of a triangle calculator?

To find the area of a triangle using a calculator, enter the base and height into the formula 1/2×base×height. Some calculators may also allow you to input side lengths and use Heron's formula or other methods.

What is the formula for area of a right triangle?

The formula for the area of a right triangle is 1/2×base×height.

How do you find the surface area of a triangle prism?

To find the surface area of a triangular prism, calculate the area of the two triangular bases and the areas of the three rectangular sides, then add them together. The formula is:

Surface Area = 2×Area of Triangle + Perimeter of Triangle × Length of Prism

How to find area of a triangle prism?

To find the area of a triangular prism, calculate the area of the triangular base using 1/2×base×height, and then use this to find the volume and surface area of the prism.

How to determine the area of a triangle?

To determine the area of a triangle, measure the base and height, then apply the formula 1/2×base×height.

What is the area of a triangle calculator?

An area of a triangle calculator is a tool that allows you to input the base and height, or the side lengths and included angles, to quickly calculate the area of the triangle.

How to measure the area of a triangle?

To measure the area of a triangle, use the formula 1/2×base×height after measuring the base and the height.

How to find area of a triangle?

To find the area of a triangle, use the formula 1/2×base×height. Measure the base and height, then apply the formula.

How to find the area of a right-angle triangle?

To find the area of a right-angle triangle, measure the two legs, which act as the base and height, and then use the formula 1/2×base×height.

How to find area of a triangle with 2 sides and an angle?

To find the area of a triangle with 2 sides and an included angle, use the trigonometric formula:

Area=1/2×a×b×sin⁡(C)

where a and b are the sides, and C is the included angle.

How to solve for the area of a triangle?

To solve for the area of a triangle, use the formula 1/2×base×height

if you know the base and height, or use Heron's formula if you know the lengths of all three sides.

How do you find the area of an equilateral triangle?

To find the area of an equilateral triangle, use the formula:

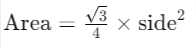
How to find area of a triangle formula?

The formula to find the area of a triangle is:

1/2×base×height